Correlation and Reliability of Two Field Tests for Vertical Jump Height
Article information
Abstract
OBJECTIVES
This study established the relationship and reliability of vertical jump height measurements using both the jump-reach method and the flight-time method.
METHODS
Sixteen healthy subjects (13 males and 3 females, body mass index: 22.5 kg/m2) visited the laboratory twice with at least two days between visits. During each visit, they performed three successful trials of one- and two-legged maximal vertical jumps on a Vertec jump tester (the jump-reach method). Simultaneously, two digital cameras were videotaped, one for a whole body view and another for a view of the feet (240 frame rate and 1/1000 s shutter speed). Flight-times were measured using a free motion analysis software (Kinovea 0.8.15) and were then inserted into the formula h = t2 × 122.625 to calculate the height. To determine if the jump values from each method were correlated, average values from the three trials for both jump methods were analyzed using Pearson correlation and simple linear regression tests. To establish a within- and between-session reliability, the intraclass correlation coefficients (ICCs) were calculated.
RESULTS
Assessed vertical jump heights using the two methods were highly correlated with each other (r values ranged between 0.86 and 0.93 with p<0.0001 for all tests) and showed high reliability (ICC values ranged between 0.73 and 0.99 for all tests).
CONCLUSIONS
Vertical jump heights assessed by the two field tests were highly correlated and consistent. Although the flight-time method calculates less jump heights, the underestimated amount can be estimated by the established equations. We suggest that athletes and coaches use either technique in the field in consideration of advantages for each method.
Introduction
Vertical jumps are common in athletic fields, not only as an essential movement (e.g., basketball and volleyball) but also as functional tests [1-5]. There are many tools and methods that can assess vertical jump performance [5-10]; examples of this are (a) tracking the vertical displacement of a body landmark [7,10], (b) measuring the velocity and impulse at take-off [9,11], (c) subtracting the body height (standing arm reach) from the jump height (jumping and reaching toward plastic vanes) [5,8], and (d) estimating the time spent in the air (flight-time) [10,12-14]. Among these, method (a) is considered the gold standard in terms of measurement accuracy [8,10].
Although tracking a landmark using a 3D motion system is recommended, such a method requires expensive equipment and trained personnel. Additionally, the processes of data collection and reduction are difficult and complex. Relatively speaking, the jump-reach method is generally simpler, thus the results can be obtained immediately after jumping [5]. However, the jump heights were measured to be 2.4 cm [11] and 4.3 cm [8] lower compared to the force platform measurement and the 3D motion system, respectively. Since this method requires the combined ability to jump and touch vanes [8], individuals with poor coordination may inadvertently have smaller measurements. The plastic vanes are also arranged in half-inch (1.27 cm) increments, thus not allowing for measurements more precise than that. The measurement reliability of the jump-reach method has also been established (within-session: ICC=0.98 and between-session: ICC=0.86) [5].
Measuring the flight-time, defined as the time between take-off and landing, is also commonly used to determine jump height [10,13,14]. Unlike the jump-reach method, subjects do not need to jump and touch any objects, and so this measurement method can be used for functional movements such as figure skating [15]. Flight-time can be recorded using a 2D digital camera [13,16], a force platform [6,17] Francisco de Villarreal, Eduardo Saez-Saez Pääsuke, Mati Reliability and validity of a wireless microelectromechanicals based system (Keimove™, or a custom-made mat [11]. Afterwards, the flight-time is inserted into a certain equation [17] to calculate the vertical jump height. However, this calculation underestimates the jump height by up to 10 cm [10]. Various reasons for this have suggested, including changes in posture [18] and differences between the ascending and descending times in air [7]. We also note that the measurement consistency is very large for this technique (within-session reliability: ICC = 0.98) [13].
Despite underreporting values, the jump-reach method and the flight-time method are still popular in both sports and research due to their practicality and strong correlation with the gold standard [8,10]. Therefore, the degree of agreement between these field tests needs to be examined. Additionally, since systematic errors in the above measurement methods primarily result from movements in the air (body coordination, crouching posture, etc.), the longer that subjects stay in the air, the higher the discrepancy in jump height. Worth noting is that the subjects in all previous studies [7,8,10,11,14,17,18] were attempting to achieve their maximal vertical jump height. Determining the correlation via simultaneous measurements at a submaximal intensity (e.g., one-legged maximal vertical jump) would reveal if the flight-time is a factor.
The purpose of this study was to determine the correlation between the jump-reach method and the flight-time method. Additionally, we evaluated whether the intensity of the vertical jump (and thus the flight-time) influences the results of both measurements. We expected the jump-reach method to produce larger measurement values than those for the flight-time method. We also expected to see a higher degree of agreement between these two methods at smaller intensities (one-legged maximal vertical jump).
Methods
Experimental Approach
For the jump-reach method, the Vertec jump tester (Sports Imports, Columbus, USA) was used. For the flight-time method, two digital cameras (Casio EX-ZR1200, Casio Computer CO., Ltd., Tokyo, Japan) and open-license motion analysis software (Kinovea 0.8.15 for Windows) was used. Subjects performed one- and two-legged vertical jumps at maximal effort in three trials for two separate sessions. The two methods simultaneously measured vertical jump height and were compared.
Participants
Sixteen healthy collegiate students volunteered (13 males and 3 females; age: 22.8 ± 1.6 year; height: 173.9 ± 7.3 cm; mass: 67.4 ± 9.2 kg; body mass index: 22.5 kg/m2). Subjects were excluded if they had pain in the lower-back or lower-extremity in the last six months or if they underwent surgery at any point in their lifetime. Subjects were asked to not consume alcohol or caffeine, or perform intensive physical activities (e.g., work out) prior to visiting. Before participation, subjects were fully informed of the testing procedures and gave informed consent approved by the university’s institutional review board.
Testing Procedures
All subjects visited the laboratory (temperature and humidity maintained at 25 °C and 50%, respectively) at the same time of day on two separate days. Upon arrival, subjects performed a warm-up exercise (riding a stationary bike for 5 min), then measured their standing arm reach on Vertec. They stood and maintained their trunk in an upright position while keeping their feet on the ground and raising their dominant arm (the arm used to throw a ball) directly overhead as high as possible. Afterwards, subjects performed one- and two-legged maximal countermovement vertical jumps on the Vertec. The dominant leg (i.e., the leg used to kick a ball) was used for one-legged jumps. Countermovement jump was defined as that vertical jump using a self-selected pre-stretch of the lower-extremity and trunk-flexion, as well as double-arm swinging at take-off, were allowed. Three trials for each type of vertical jump were recorded, with a 45-s rest between each jump. Vertical jump heights were calculated by subtracting the height of the standing arm reach from the jump height. Values were recorded in inches, then converted to cm (i.e., multiplying by 2.54).
While subjects were performing vertical jumps on the Vertec, two digital cameras (sampling rate: 240 fps; shutter speed: 1/1000 s; resolution: 512 × 384 pixels) simultaneously videotaped the subjects’ feet (camera 1) and whole bodies (camera 2: Figure 1). Two extra light emitting diodes (Power Line, Focus Global, Korea: 10.5 × 10.5 × 18 cm; 2,400 lm) were placed 60 cm away from the jump and landing spot [Figure 1]. Recorded video clips taken with the two cameras were synchronized using Kinovea. Afterwards, number of frames (starting from the take-off frame measured through the landing frame) were counted to determine the flight-time, which was then used to calculate the jump height according to the equation h = t2 × 122.625 (h: jump height in cm; t: fight time in s) [17].
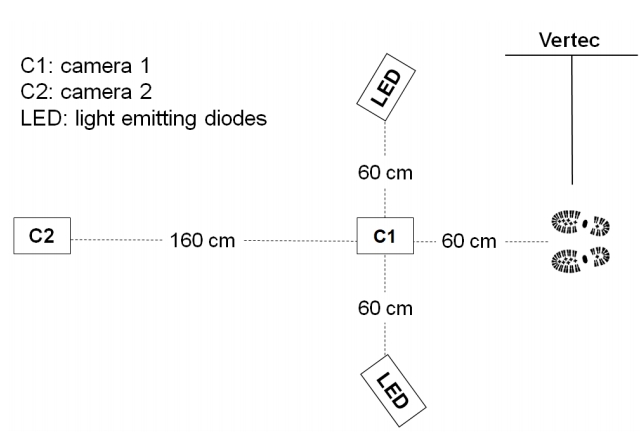
Apparatus for vertical jump measurements.
Camera 1 (C1) was located on the ground to capture the subject’s foot (feet) and camera 2 (C2) was located 1 m above the ground to videotape the whole body. Two light-emitting diode lights (L) were used to enhance the brightness of the jumping and landing spot.
Subjects repeated the same procedures on the second visit with at least two days between-sessions.
Statistical Analysis
When considering data for maximal vertical jump height from a previous study [19], 15 subjects were necessary (an effect size of 0.83 and a statistical power of 0.80).
The average and standard deviation of three trials of vertical jump height for each jump type, method, and session were calculated. To determine the relationship between these methods, we used the Pearson correlation coefficient and simple linear regression tests. In these simple linear regressions, the values measured by the flight-time method were set as the independent variable (y). We also calculated the between-method Cohen’s d effect size (ES) for each intensity.
To calculate the measurement consistency, the collected data were analyzed using mixed-model ANOVAs. Once the between-subjects mean square (BMS) and the error mean square (EMS) values were obtained, the reliabilities of each jump type, both within- and between-session, were calculated using the following equation: ICC = [BMS–EMS] / BMS [20]. The standard error of measurement (SEM) for each value was also calculated using the following equation: SEM = SD × √1 – ICC [21].
All data were analyzed using the statistical package SAS 9.4 (SAS institute Inc., NC, Cary, USA).
Results
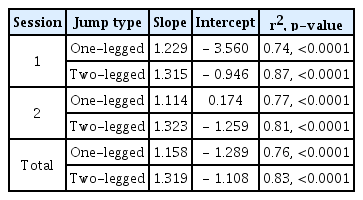
The Pearson correlation coefficient showed that the two measurement methods were highly correlated [Table 1]. Calculated r values were the lowest at 0.86 with one-legged jump and the highest at 0.93 with two-legged jump (p<0.0001 for all tests) performed in the first session. The slopes and intercepts for each comparison and related values in r2 and p-values are presented in Table 2.
The jump height values measured via the flight-time method were smaller than those for the jump-reach method [Table 3]. The difference ranged between 8.2 cm and 9.9 cm (an average of 9.2 cm).
High measurement consistency (ICC values ranged from 0.85 to 0.99) was calculated in both with- and between-session [Table 3].
Discussion
The primary purposes of our study were to determine how the values for these two methods are correlated and to examine if jump intensity affects the differences in jump height. The jump height values for each method were highly correlated, as reported by many previous studies [8,11,22,23]. The coefficient of determination (r2) ranged from 0.74 to 0.87 [Table 1]. This indicates that at least 74% up to 87% of the variation in one method is explained by the variation in the other. Despite the strong correlation, the mean values differed by 8.2 to 9.9 cm [Table 3]. Since jump height and measurement error are proportional [13], we expected that the jump height of one-legged jumps would show a greater degree of agreement between the two methods. Interestingly, however, our data showed a similar correlation between two measurement techniques.
Previously, the flight-time method was validated using the force platform [16] and OptoJump IR platform [13] as references. Both studies reported average differences of 0.1 ms [16] and 2.1 ms [13] in flight-time, which is negligible since a flight-time of 2.1 ms yields a jump height difference of 0.1 cm. The sampling rate in each study was 500 Hz [16] and 240 Hz [13]. Our study used parameters similar to those in the second study [13], except for the shutter speed (1/4000 s; we used 1/1000 s) and resolution (448 × 336 pixels; we used 512 × 318 pixel). However, we observed a large difference (up to 10 cm) compared to the values using the Vertec. We heavily controlled the systematic error for flight-time measurements by: synchronizing two video clips and confirming take-offs/ landings; using higher quality images; using extra lights on the floor; and having a trained observer. Assuming that our method had minimal systematic errors, the results of our study suggest that flight-times measured via 2D camera-based techniques underestimate vertical jump height.
The two field tests examined in this study are simple in the sense that they do not require data reduction in kinetics or kinematics. Comparing these two tests, the jump-reach method requires handling a tall and heavy structure while the flight-time method uses small digital cameras and a tripod. However, the flight-time method takes a longer time to process data and can be influenced by an environmental condition such as rain or snow. Since the values from the flight-time method are underreported but with a consistent relationship, the equations developed using the slopes and intercepts of our study [Table 2] may be used to estimate the values that would have been obtained using the jump-reach method. As an example, we show the case for two-legged maximal vertical jumps, considering the value of 35 cm from the flight-time method:
Jump height = [1.319 × (value from the flight-time method)] – 1.108 = (1.319 × 35) – 1.108 = 45.1 cm.
Using the slopes and intercepts in Table 2, the flight-time for each jump height measurement on the Vertec can also be estimated. As an example, consider the height of 44 cm for the jump-reach method:
Flight-time = √[10000 × (value from the Vertec + 1.108)] / 1319 = √[10000 × (45.108)] / 1319 = 0.509 s.
This study did not include a concurrent gold standard measurement with the two field tests. For example, if our measurement protocols were conducted on the force platform along with the 3D motion capture system, the results would have determined the degree of agreement on each field test relative to the reference test. While we admit that this might be a limitation of our study, the methods and results of our study are useful in the athletic field since each of the two field test (the jump-reach [8] and the flight-time [13] methods) has previously been validated.
Conclusions
Vertical jump heights assessed by the two field tests were highly correlated and consistent. Although the flight-time method calculates less jump heights, the underestimated amount can be estimated by the established equations. We suggest that athletes and coaches use either technique in the field in consideration of advantages for each method.
Notes
The authors declare no conflict of interest.